Sailing Hydrofoils and the Fold Catastrophe

What floats your boat?

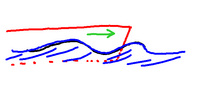
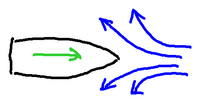
Pushing water out of the way Sitting in a hole A simple bow wave Climbing a mountain Archimedes' Principle tells us that a boat floats because it displaces water. The force required to push and hold the water out of the way as the boat is lowered into the water, is (by Newton's principle of equal and opposite forces) the same as the force exerted by the water to hold the boat up. However, as the boat starts to move, it has to push water out of the way. This means that the water piles up on either side of the bow (the pointy end) and that creates the bow wave that we can see so clearly as a boat travels. Not surprisingly, the faster you go, the larger the bow wave becomes. The larger bow wave in turn has a longer wave length (partly because of the boat's speed), and after a certain point the wavelength equals (or exceeds) the length of the boat. In effect, the boat has created a hole in which it sits. The deeper sitting boat now has even more water to push out of the way, and ends up having to climb a mountain of its own making.

On the plane So to make a boat go faster we need to do two things. Firstly, make the boat thin so that it doesn't have to push much water out of the way. Secondly, make it long so it doesn't fall in the hole. For many, many years it was thought that to be fast, boats had to be long and thin. Then the idea of planing arose. When planing a boat is no longer displacing water, it's skipping over the top. Some of its "lift" comes from the dynamic force of the water hitting the bottom of the hull, and so less water has to be forced out of the way. Less pushing, less bow wave, more speed. To get up "on the plane", though, boats have to go fast, and must be light. It requires enormous amounts of power to get a large, heavy boat up onto the plane and keep it there.

The need for speed

But there's another way to go fast on water. It's been around for a while, but it's coming into its own. Make it fly! In September 2009 the sailing hydrofoil l'Hydroptère broke the world speed sailing record (subject to ratification) with an average speed of 51.36 knots over 500 meters, and hitting a peak speed of 55.7 knots. But underneath this amazing scientific and technological feat lies a mathematical catastrophe. So what are hydrofoils? In essence, hydrofoils are wings designed to work in water. As with aeroplane wings, a combination of deflecting the water and altering the speed - hence the pressure - provides a lifting force, raising the boat from the water. The foils themselves create drag, but at speed, there is less drag from the foils than from the hull. The exact balance of these differing effects is intriguing. So let's have a closer look at it.

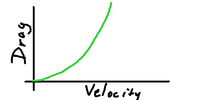
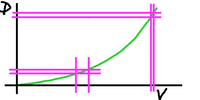
In general, anything moving suffers from drag. The faster you go, the more drag you experience.

To a first approximation, your drag goes up with the square of your velocity, as roughly shown here.

The exact amount of drag depends on your shape (as well as other factors). More streamlining usually results in less drag, while being big and boxy results in more drag. Your shape does not change the shape of the drag/velocity curve, but it does change the steepness of the curve. The red curve might be for a large truck, and the blue line for a sports car.

So for any velocity, we've marked one here, (although I haven't yet - the diagram needs updating!) you can see that the red line is higher than the blue line. A less streamlined shape suffers more drag.

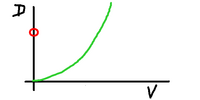
But let's ask the reverse (actually "converse") question. For a given amount of drag, how fast are we going? This is interesting because the drag controls our maximum speed when we have a given amount of driving power. When we travel at a constant speed, the drag must be exactly balanced by the driving force. So if we say how much power we can supply, that will be the amount of drag. Start from that level on the diagram, move across to the curve, then down to the X axis and we can see how fast we can travel, given that amount of power.

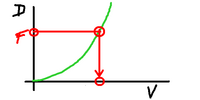
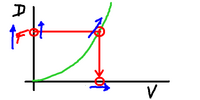
If we supply a little more power then we will accelerate. The force supplied goes up, and the velocity goes up taking with it the amount of drag we experience. When that matches the new amount of driving force, we are again balanced. The same thing happens if we reduce our driving force. We no longer have enough power to overcome the drag, we slow a little, the drag reduces and again we are in balance.

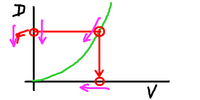
In short, by varying slightly the power provided we adjust our speed. At low speeds, small changes in the power can give larger changes in the speed, while at high speeds, small changes in the power only result in very small changes in the speed. And we can see this by looking at the slope of the curve. The gradient is much larger at higher speeds than at lower speeds. The equations for the velocity/drag curve allow precise analyses, but we won't go into that much detail here.

This needs a better diagram.

Now we complicate things

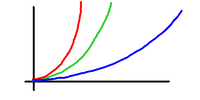
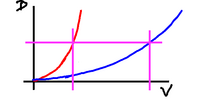
Now let's look at a sailing hydrofoil. This has two different curves at the same time (sort of). When travelling with the hull in the water the drag is very large, because there's not just the hull, but there are also the hydrofoils to push through the water. For that mode, we have the red line. A little velocity and the drag shoots up. But when flying, the drag is very small. In that case we use the blue velocity/drag curve. Much to be preferred. Even though we're travelling fast there isn't much drag. The truck is now a sports car.

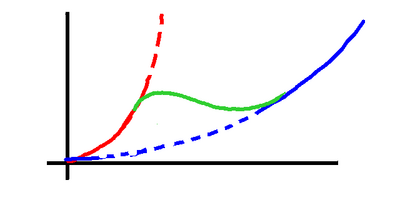
So here's what happens. To start with it's tough to get going, but as we pick up speed the foils start to lift the hull. The increase in drag from the foils continues, of course, but the drag from the hull falls away even faster, and so the total drag peaks, then decreases while the hull is being lifted out, and then starts to rise again. We move from "truck" mode to "sports" mode, so we move from the red line to the blue line. The green line shows the transition. Typically "lift-off" can happen at 4 to 6 knots of speed, which is achievable in around 10 knots of wind. Once flying the craft can typically travel at 1.5 to 2 times the speed of the wind.

You may be wondering how a sailing vessel can go faster than the wind. It's all to do with angles and trigonometry, and although it's not hard, this article is already complicated enough.

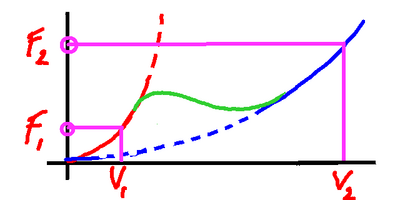
So when we've not got much power and we're travelling slowly, we're travelling really slowly. But when we have more power and get over the transition, we are travelling much, much faster. We can see here with driving force F1 we travel at speed V1, but with force F2 we can travel at speed V2

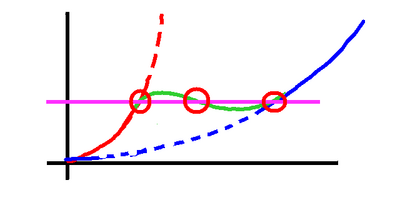
But what about in between? Here we have a driving force in between. We've put the line across at the amount of drag that balances our driving force, and we ask "How fast are we travelling?" The problem is that there appear to be three answers!

The exciting bit!

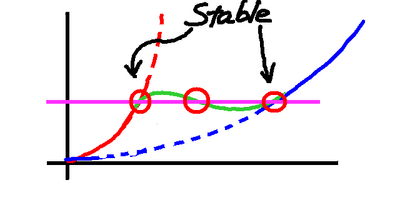
Not all answers are equal. We can see that the slowest and the fastest really just look like the earlier cases of the truck and the sports car. Nothing interesting there. Add a little power, increase a little in speed, and everything is back in balance.

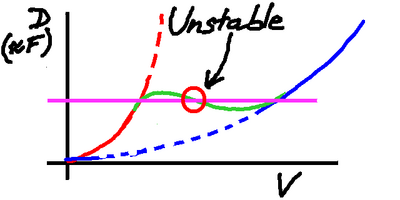
But what's happening in the middle case? So far we've been equating Force supplied with drag, because a little more force gives a little more speed which gives a little more drag to balance the power, and all remains stable. Here, it's radically different.

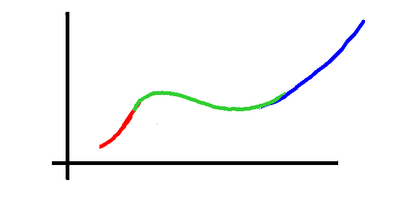
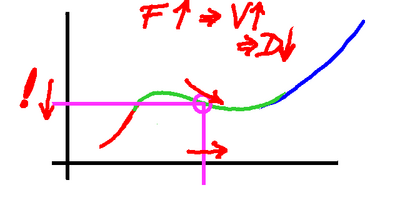
In the middle section, shown here in green, the velocity/drag curve slopes downwards, and that makes all the difference. Now if we provide a little more power we speed up, having more power than drag. But as we go faster we get less drag, so the imbalance increases, and we go faster and faster, until finally we're going fast enough that the drag is increasing again, and at last catches up. So in this section we no longer have the expected relationship between drag and force. Instead we find that an increase in force causes an increase in speed which causes a decrease in drag, which creates even more acceleration.

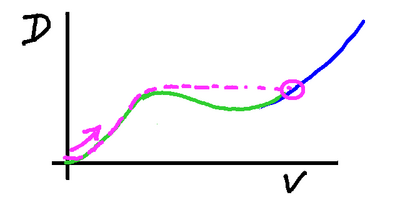
So starting from a gentle roll we slowly build speed, increasing gently until we get towards the turning point of the curve. Suddenly we get positive feedback and our speed snaps up with enormous acceleration, until finally we balance out again on the blue part of the curve. Plotting drag versus velocity is no longer giving us the information we want. Really, we want to start with the driving force available, and work out how fast we'll be able to travel. We need to turn our graph around.

Speed as a result of power

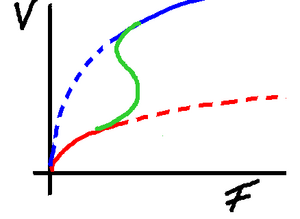
So here we have drawn the same graph, but now we have velocity as the result, running up the Y-axis, and we have Force along the X axis. Previously we were looking at drag, but once the system is in equilibrium force and drag are balanced. It makes sense, therefore, to consider the velocity we get as a result of a given driving force.

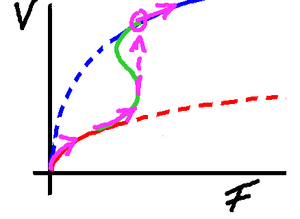
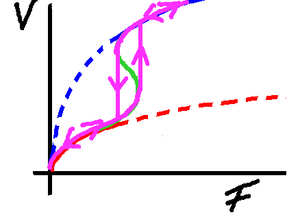
Here we can see that as we slowly increase the driving force so we climb the red curve. But as the hull starts to rise from the water and our drag decreases we have a sudden leap in speed. We find ourselves flying, having gone through a discontinuity in the Force/Velocity curve. Typically take-off will happen in 10 knots of wind, and the craft will accelerate from 5 kts to 15 or 20 kts in the space of a couple of boat lengths. Dramatic indeed!

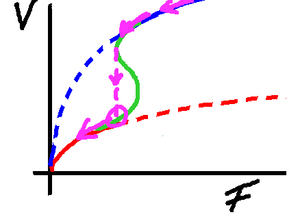
Slowing back down it's the same, only in reverse, and note that the discontinuity happens at a different place. Now we stay on the upper curve - we remain flying - until the hull touches the water and we slow with a very rapid deceleration, often accompanied by a massive splash!

So here is the profile of a complete cycle. It starts from rest, applies increasing driving force until the vessel achieves "take-off" whereupon it accelerates rapidly to a cruising speed. As the driving force is then slowly reduced the speed decreases smoothly until the hull touches the water and the vessel slows rapidly. Of course, the discontinuities aren't jump discontinuities, the vessel has a mass, so the curve is, in reality, more smooth than this graph might lead you to believe. However, the sudden acceleration and deceleration are very real.

Different craft, different curves

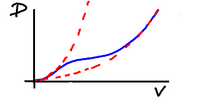
It's possible that a particular craft doesn't exhibit the dramatic change, transitioning more gently from one mode to another. Much less fun. We can overlay the drag/velocity curves for craft with different characteristics on a single graph.

However, it can be easier to visualise if we separate the curves in the third dimension to create a surface. Here we have a surface, with the most dramatic version in the front, and the less dramatic version at the back, with a smooth transition between them. A vertical slice parallel to the screen gives a single Power/Speed graph, and therefore corresponds to a single vessel's characteristics. The graph shows that in many places, that is, combinations of design and windspeed/power, there is a single resulting stable speed. But it also shows that there are areas where there is more than one possible speed, depending on whether the craft is on foils or in displacement mode. The graph also shows that by moving around in a continuous manner, the system behaviour can nevertheless be discontinuous. A sudden leap or loss of speed can occur when we move from an area with more than one stable speed to an area with only one.

We use mathematics to understand systems where stable points of equilibrium can appear and disappear as input parameters change. Such systems can show discontinuities in their output, even though the inputs have been changed smoothly, and by small amounts. By studying such systems, we can hope to classify the circumstances under which they occur, and possibly anticipate, or even prevent, undesirable "catastrophic" changes. Hence the name of this field of study: "Catastrophe Theory."

Enthusiasts point to discontinuous behaviour that can turn up in stock markets, crowd behaviour, markets, and other places, and wonder whether the study of Catastrophe Theory may one day find direct application in such fields. What we've shown here is that simple examples really do turn up in real life.